Note: This tutorial was generated from an IPython notebook that can be downloaded here.
Quickstart¶
This notebook was made with the following version of emcee:
import emcee
emcee.__version__
'0.3.0.dev0'
The easiest way to get started with using emcee is to use it for a project. To get you started, here’s an annotated, fully-functional example that demonstrates a standard usage pattern.
How to sample a multi-dimensional Gaussian¶
We’re going to demonstrate how you might draw samples from the multivariate Gaussian density given by:
where \(\vec{\mu}\) is an \(N\)-dimensional vector position of the mean of the density and \(\Sigma\) is the square N-by-N covariance matrix.
The first thing that we need to do is import the necessary modules:
import numpy as np
Then, we’ll code up a Python function that returns the density
\(p(\vec{x})\) for specific values of \(\vec{x}\),
\(\vec{\mu}\) and \(\Sigma^{-1}\). In fact, emcee actually
requires the logarithm of \(p\). We’ll call it log_prob:
def log_prob(x, mu, icov):
diff = x - mu
return -0.5*np.dot(diff,np.dot(icov,diff))
It is important that the first argument of the probability function is
the position of a single “walker” (a N dimensional numpy array).
The following arguments are going to be constant every time the function
is called and the values come from the args parameter of our
EnsembleSampler that we’ll see soon.
Now, we’ll set up the specific values of those “hyperparameters” in 5 dimensions:
ndim = 5
np.random.seed(42)
means = np.random.rand(ndim)
cov = 0.5 - np.random.rand(ndim ** 2).reshape((ndim, ndim))
cov = np.triu(cov)
cov += cov.T - np.diag(cov.diagonal())
cov = np.dot(cov,cov)
and where cov is \(\Sigma\). Before going on, let’s compute the
inverse of cov because that’s what we need in our probability
function:
icov = np.linalg.inv(cov)
It’s probably overkill this time but how about we use 250 walkers? Before we go on, we need to guess a starting point for each of the 250 walkers. This position will be a 50-dimensional vector so the initial guess should be a 250-by-50 array—or a list of 250 arrays that each have 50 elements. It’s not a very good guess but we’ll just guess a random number between 0 and 1 for each component:
nwalkers = 250
p0 = np.random.rand(nwalkers, ndim)
Now that we’ve gotten past all the bookkeeping stuff, we can move on to
the fun stuff. The main interface provided by emcee is the
EnsembleSampler object so let’s get ourselves one of those:
sampler = emcee.EnsembleSampler(nwalkers, ndim, log_prob, args=[means, icov])
Remember how our function log_prob required two extra arguments when
it was called? By setting up our sampler with the args argument,
we’re saying that the probability function should be called as:
log_prob(p0[0], means, icov)
-2.5960945890854434
If we didn’t provide any args parameter, the calling sequence would
be log_prob(p0[0]) instead.
It’s generally a good idea to run a few “burn-in” steps in your MCMC
chain to let the walkers explore the parameter space a bit and get
settled into the maximum of the density. We’ll run a burn-in of 100
steps (yep, I just made that number up… it’s hard to really know how
many steps of burn-in you’ll need before you start) starting from our
initial guess p0:
pos, prob, state = sampler.run_mcmc(p0, 100)
sampler.reset()
100%|██████████| 100/100 [00:00<00:00, 305.62it/s]
You’ll notice that I saved the final position of the walkers (after the
100 steps) to a variable called pos. You can check out what will be
contained in the other output variables by looking at the documentation
for the EnsembleSampler.run_mcmc() function. The call to the
EnsembleSampler.reset() method clears all of the important
bookkeeping parameters in the sampler so that we get a fresh start. It
also clears the current positions of the walkers so it’s a good thing
that we saved them first.
Now, we can do our production run of 10000 steps:
sampler.run_mcmc(pos, 10000);
100%|██████████| 10000/10000 [00:24<00:00, 407.28it/s]
The sampler now has a property EnsembleSampler.chain that is a
numpy array with the shape (1000, 250, 50). Take note of that shape
and make sure that you know where each of those numbers come from.
Another useful object is the EnsembleSampler.flatchain which
has the shape (250000, 50) and contains all the samples reshaped
into a flat list. You can see now that we now have 250 000 unbiased
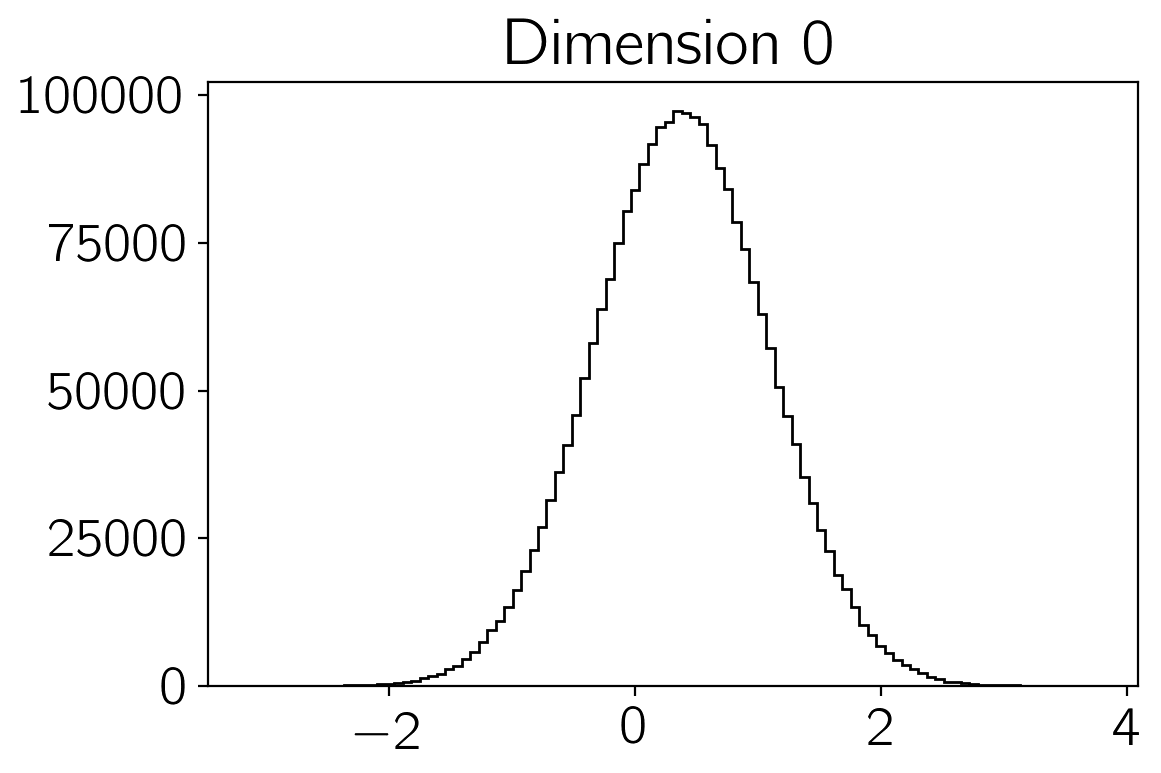
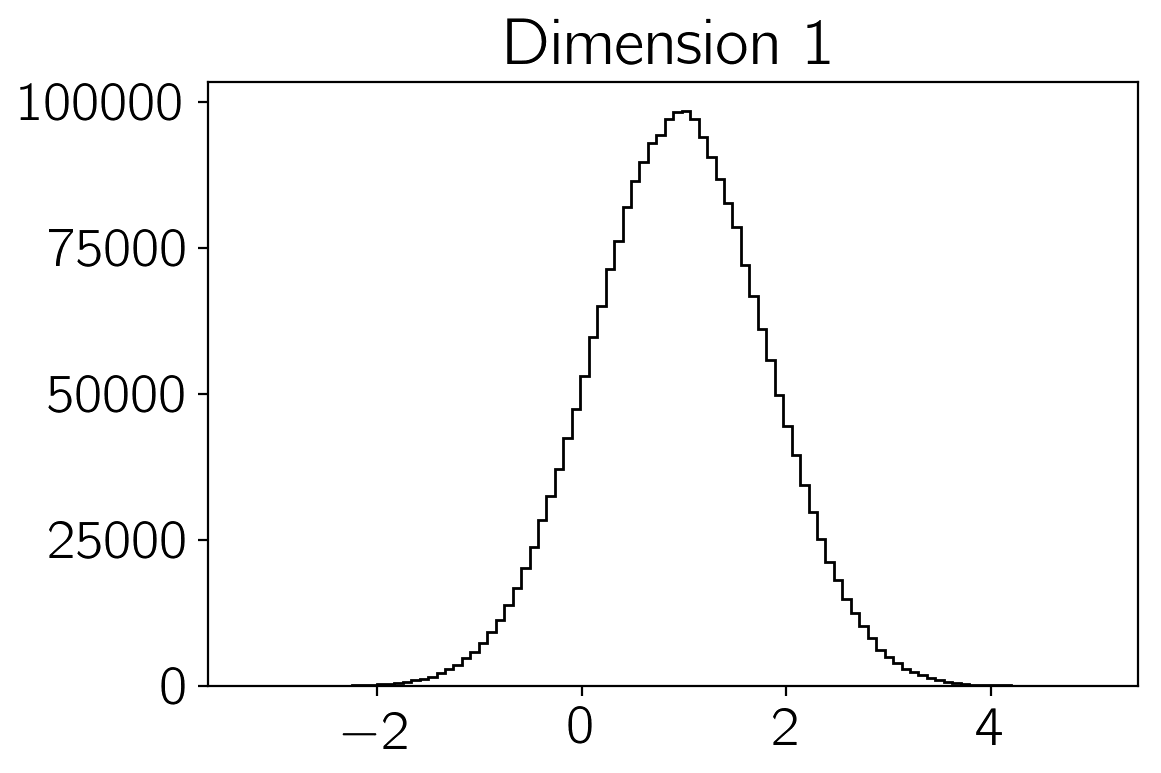
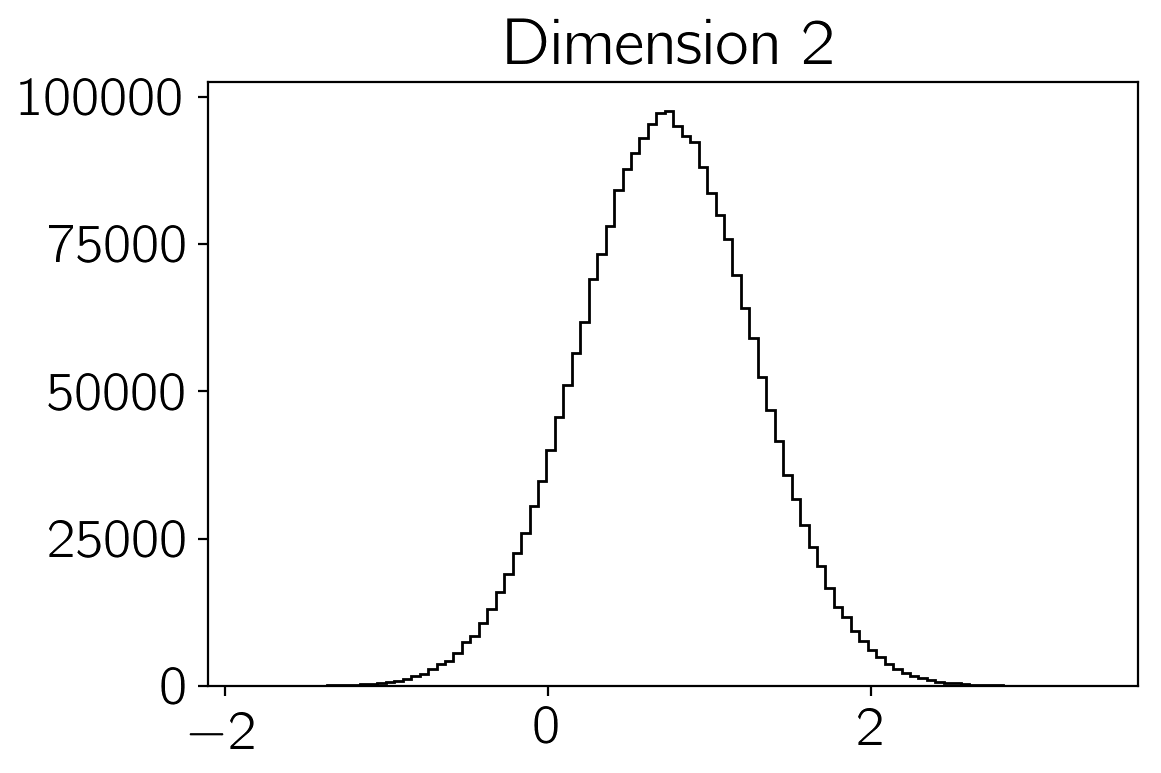
samples of the density \(p(\vec{x})\). You can make histograms of
these samples to get an estimate of the density that you were sampling:
Autocorrelation analysis & convergence
sampler.get_autocorr_time()
array([ 54.61620237, 53.72668829, 54.67029465, 54.80001017, 53.99357549])
import matplotlib.pyplot as plt
for i in range(3):
plt.figure()
plt.hist(sampler.flatchain[:,i], 100, color="k", histtype="step")
plt.title("Dimension {0:d}".format(i))
Another good test of whether or not the sampling went well is to check
the mean acceptance fraction of the ensemble using the
EnsembleSampler.acceptance_fraction() property:
print("Mean acceptance fraction: {0:.3f}"
.format(np.mean(sampler.acceptance_fraction)))
Mean acceptance fraction: 0.551
This number should be between approximately 0.25 and 0.5 if everything went as planned.
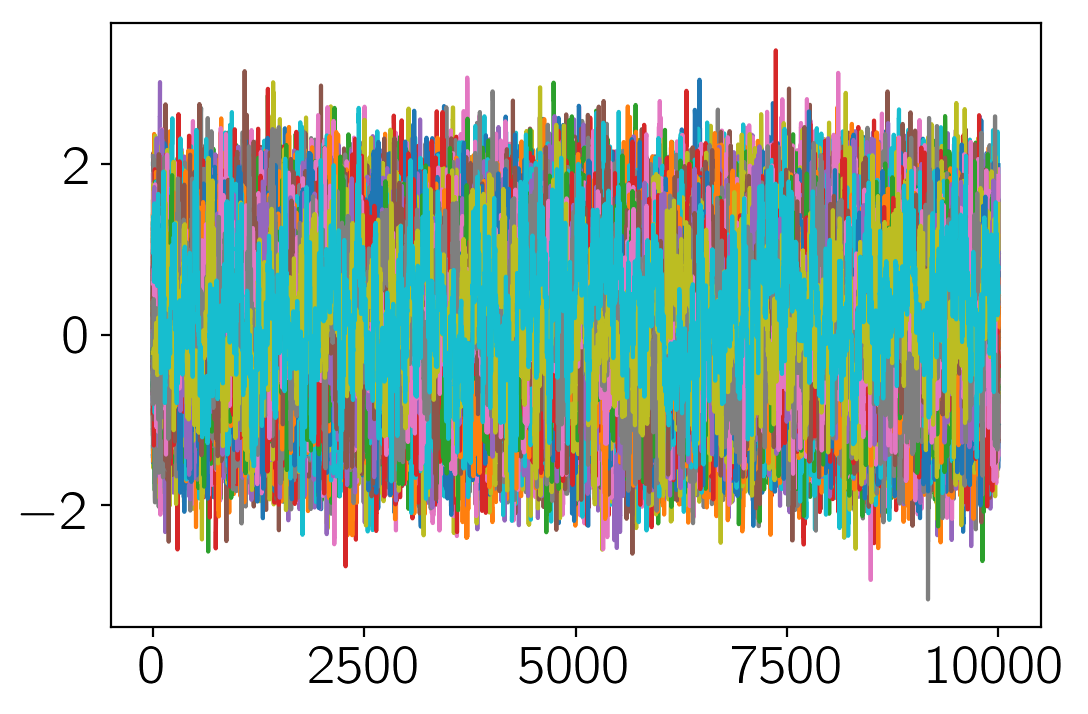
plt.plot(sampler.chain[:, :, 0]);
plt.plot(sampler.chain[:, :, -1]);